
Otto Dix The Triumph of Death 1934
Yes, austerity really kills real people, and it kills the societies they live in. Let’s try and explain this in simple terms. It’s a simple topic after all. Austerity is a mere left-over from faith-based policies derived from shoddy economics, and economics is a shoddy field to begin with. The austerity imposed on and in several countries and their economies after 2008, and the consequences it has had in these economies, cannot fail to make you wonder what level of intelligence the politicians have who did the imposing, as well as the economists who advised them in the process.
We should certainly not forget that the people who make these decisions are never the ones affected by them. Austerity hurts the poor. For those who are living comfortably -which includes politicians and economists that “matter”-, austerity at worst means eating and living somewhat less luxuriously. For the poor, taken far enough, it will mean not eating at all, not being able to afford clothing, medical care, even housing. Doing without 10% of very little hits much harder than missing out on 10% of an abundance.
And even then there are differences, for instance between countries. The damage done to British housing, education and health care by successive headless chicken governments is very real, and it will require a huge effort to restore these systems, if that is possible at all. Still, if the British have any complaints about the austerity unleashed upon them, they should really take a look at Greece. As this graph of households having a hard time making ends meet makes painfully clear:
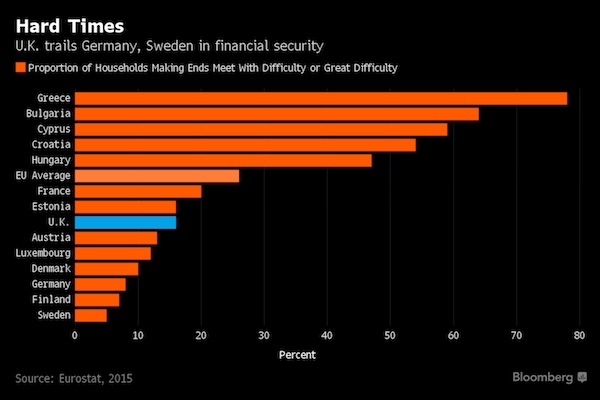
Britain ‘only’ suffers from economically illiterate politicians and economists. Greece, on top of that, has to cope with a currency it has no control over, and with the foreign -dare we say ‘occupying’?- powers that do. A currency that is geared exclusively to the benefit of the richer Eurozone nations. The biggest mistake in building the EU, and the Eurozone in particular, is that the possibility has been left open for the larger and richer nations to reign over the smaller and poorer almost limitlessly. These things only become clear when things get worse, but then they really do.
This ‘biggest mistake’ predicted the end of the ‘union’ from the very moment it was established; all it will take is time, and comprehension. Eurozone rules say a country’s public debt cannot exceed 60% and its deficit must remain less than 3%. Rules that have been broken left right and center, including by the rich, Germany, France, who were never punished for doing so. The poor are.
These limits are completely arbitrary. They come from the text books of the same clueless cabal of economists that the entire Euro façade is based on. The same cabal also who now demand a 3.5% Greek budget surplus into infinity, the worst thing that can happen to an already impoverished economy, because it means even more money must flow out of an entity that already has none.
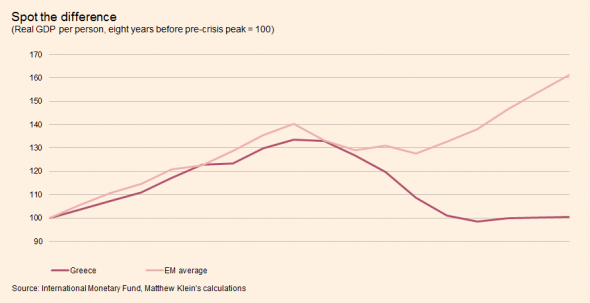
But let’s narrow our focus to austerity itself, and what makes it such a disaster. And then after that, we’ll take it a step further. We can blame economists for this mess, and hapless politicians, but that’s not the whole story; in the end they’re just messenger boys and girls. First though, here’s what austerity does. Let’s start with Ed Harrison talking about some revealing data that Matt Klein posted on FT Alphaville about comparing post-2008 Greece to emerging economies:
Europe’s Delusional Economic Policies
Here’s how Matt put it: “Greece had a very different post-crisis experience: it never recovered. By contrast, all the other countries were well past their pre-crisis peak after this much time had elapsed. On average, Argentina, Brazil, Indonesia, Thailand, and Turkey have outperformed Greece by more than 40 percentage points after nine years.”
“.. unlike those countries, Greece lacked the ability to use the exchange rate as a shock absorber. So while Brazil and Greece faced the same type of downturn in dollar terms – about 45% in GDP per person – Brazilian living standards only deteriorated about 2%, compared to 26% in Greece. The net effect is that Greece had a relatively typical crisis in dollars but an unprecedently painful one in the terms that matter most”.
[..] Greece doesn’t have its own currency so the currency can’t depreciate. Greece must use the internal devaluation route, which makes its labor, goods and services cheaper through a deflationary path – and that is very destructive to demand, to growth, and to credit.
[..] it’s not about reforms, people. It’s about growth. And the euro – and the policies tied to membership – is anti-growth, particularly for a country like Greece that is forced to hit an unrealistic 3.5% primary surplus indefinitely.
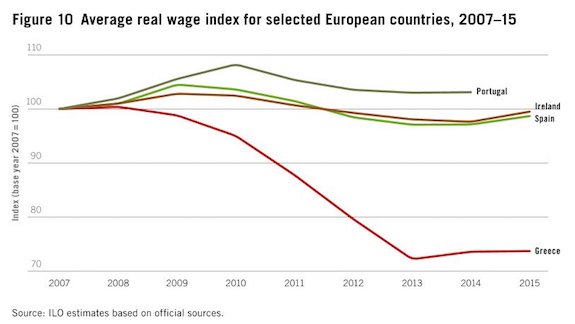
Another good report came from the WaPo at about the same time Ed wrote his piece, some 4 weeks ago. After Matt Klein showing how hard austerity hit Greece compared to emerging economies, Matt O’Brien shows us how austerity hit multiple Eurozone countries, compared to what would have happened if they had not cut spending (or introduced the euro). It is damning.
Austerity Was A Bigger Disaster Than We Thought
Cutting spending, you see, shouldn’t be a problem as long as you can cut interest rates too. That’s because lower borrowing costs can stimulate the economy just as much as lower government spending slows it down. What happens, though, if interest rates are already zero, or, even worse, you’re part of a currency union that means you can’t devalue your way out of trouble? Well, nothing good.
House, Tesar and Proebsting calculated how much each European economy grew — or, more to the point, shrank — between the time they started cutting their budgets in 2010 and the end of 2014, and then compared it with what actually realistic models say would have happened if they hadn’t done austerity or adopted the euro.
According to this, the hardest-hit countries of Greece, Ireland, Italy, Portugal and Spain would have contracted by only 1% instead of the 18% they did if they hadn’t slashed spending; by only 7% if they’d kept their drachmas, pounds, liras, escudos, pesetas and the ability to devalue that went along with them if they hadn’t become a part of the common currency and outsourced those decisions to Frankfurt; and only would have seen their debt-to-GDP ratios rise by eight percentage points instead of the 16 they did if they hadn’t tried to get their budgets closer to being balanced.
In short, austerity hurt what it was supposed to help, and helped hurt the economy even more than a once-in-three-generations crisis already had.
[..] the euro really has been a doomsday device for turning recessions into depressions. It’s not just that it caused the crisis by keeping money too loose for Greece and the rest of them during the boom and too tight for them during the bust. It’s also that it forced a lot of this austerity on them. Think about it like this. Countries that can print their own money never have to default on their debts – they can always inflate them away instead – but ones that can’t, because, say, they share a common currency, might have to.
Just the possibility of that, though, can be enough to make it a reality. If markets are worried that you might not be able to pay back your debts, they’ll make you pay a higher interest rate on them – which might make it so that you really can’t.
In other words, the euro can cause a self-fulfilling prophecy where countries can’t afford to spend any more even though spending any less will only make everything worse.
That’s actually a pretty good description of what happened until the ECB belatedly announced that it would do “whatever it takes” to put an end to this in 2012. Which was enough to get investors to stop pushing austerity, but, alas, not politicians. It’s a good reminder that you should never doubt that a small group of committed ideologues can destroy the economy. Indeed, it’s the only thing that ever has.
So those are the outcomes, But what’s the theory, where does the “small group of committed ideologues” go so wrong? Let’s go really basic and simple. Last week, Britsh economist Ann Pettifor, promoting her new book “The Production of Money: How to Break the Power of Bankers”, said this to Vogue:
Politicians who advocate for austerity measures—cutting spending—like to say that the government ought to run its budget the way women manage our households, but unlike us, the government issues currency and sets interest rates and so on, and the government collects taxes. And if the government is managing the economy well, it ought to be expanding the numbers of people who are employed and therefore paying income tax and tax on purchases—purchases that turn a profit for businesses which then hire more employees, and on and on it goes. That’s called the multiplier effect, and for 100 years or so, it’s been well understood. And it’s why governments should invest not in tax breaks for wealthy people, but in initiatives like building infrastructure.
Around the same time, Ann wrote in the Guardian:
[..] the public are told that cuts in spending and in some benefits, combined with rises in income from taxes will – just as with a household – balance the budget. Even though a single household’s budget is a) minuscule compared to that of a government; b) does not, like the government’s, impact on the wider economy; c) does not benefit from tax revenues (now, or in the foreseeable future); and d) is not backed by a powerful central bank. Despite all these obvious differences, government budgets are deemed analogous (by economists and politicians) to a household budget.
[..] If the economy slumps (as in 2008-9) and the private sector weakens, then like a see-saw the public sector deficit, and then the debt, rises. When private economic activity revives (thanks to increased investment, employment, sales etc) tax revenues rise, unemployment benefits fall, and the government deficit and debt follow the same downward trajectory. So, to balance the government’s budget, efforts must be made to revive Britain’s economy, including the indebted private sector.
In other words, when faced with economic hard times, a government should not cut spending, it should increase it -and it can-. Because cutting spending is sure to make things worse. At the same time of course, this is not an option available to Greece, because it has ceded control of its currency, and therefore its economy, to a largely unaccountable and faceless cabal that couldn’t care less what happens in the country.
All they care about is that the debts the banks in the rich part of the eurozone incurred can be moved onto someone else’s shoulders. Which is where -most of- Greece’s crisis came from to begin with. And so, yes, Germany and Holland and France are sitting sort of pretty, because they prevented a banking crisis from happening at home; they transferred it to Greece’s pensioners and unemployed youth. The ‘model’ of the Eurozone allows them to do this. Coincidence? Bug or feature?
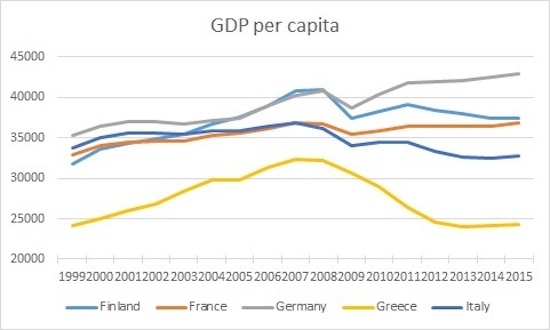
Oh, and it’s not only Greece, though it’s by far the hardest hit. Read Roberto Centeno in the Express below. Reminds me of Greeks friends saying: “In 2010, we were told we had €160 billion or so in debt, and we needed a bailout. Now we have over €600 billion in debt, they say. How is that possible? What happened? What was that bailout for?”
‘Spain Is Ruined For 50 Years’
A leading Spanish economist has hit out at the ECB saying “crazy” loans will ruin the lives of the population for the next 50 years. And it is only a matter of time before the Government is forced to default as a debt bubble and low wages effectively forge the worst declines in “living memory”. Leading economist Roberto Centeno, who was an advisor to US president Donald Trump’s election team on hispanic issues, says the country has borrowed €603 billion that it cannot conceivably pay back. And he says Spanish politicians including Minister of Economy Luis de Guindos are “insulting their intelligence” after doing back door deals with the ECB. In a blog post Mr Centeno says there needs to be audits so the country can understand the magnitude of its debt mountain.
He said Spain was “moving steadily towards the suspension of payments which is the result of out of control public waste, financed with the largest debt bubble in our history, supported by the ECB with its crazy policy of zero interest rate expansion and without any supervision.” The expert added the doomed situation will “lead to the ruin of several generations of Spaniards over the next 50 years”. [..] He said the country is currently suffering from a “third world production model”. He added: “We have a third world production model of speculators and waiters, with a labour market where the majority of jobs created are temporary and with remunerations of €600, the largest wage decline in living memory. “And all this was completed with a broken pension system and an insolvent financial system.”
Forecasting an unprecedented shock to the European financial model, Mr Centento is calling for an immediate audit despite a recent revelation that the ECB is failing in its supervisory role over Europe’s banks. He also claimed the Spanish government and European Union leaders have been manipulating figures since 2008. Mr Centento said: “We will require the European Commission and Eurostat to audit and audit the Spanish accounting system for serious accounting discrepancies that may jeopardise stability. “The gigantic debt bubble accumulated by irresponsible governments, and that never ceases to grow, will be the ruin of several generations of Spaniards. “The Bank of Spain’s debt to the Eurosystem is the largest in Europe. “The day that the ECB minimally closes the tap of this type of financing or markets increase their risk aversion, the situation will be unsustainable.”
But then it’s time to move on, courtesy of Michael Hudson, prominent economist, who should be a guest of honor, at the very least, at every Eurogroup meeting. You know, to give Dijsselbloem and Schäuble a reality check. Michael shines a whole different additional light on European austerity policies. This is from an interview with Sharmini Peries:
Finance as Warfare: IMF Lent to Greece Knowing It Could Never Pay Back Debt
MICHAEL HUDSON: You said the lenders expect Greece to grow. That is not so. There is no way in which the lenders expected Greece to grow. In fact, the IMF was the main lender. It said that Greece cannot grow, under the circumstances that it has now. What do you do in a case where you make a loan to a country, and the entire staff says that there is no way this country can repay the loan? That is what the IMF staff said in 2015.
It made the loan anyway – not to Greece, but to pay French banks, German banks and a few other bondholders – not a penny actually went to Greece. The junk economics they used claimed to have a program to make sure the IMF would help manage the Greek economy to enable it to repay. Unfortunately, their secret ingredient was austerity.
[..] for the last 50 years, every austerity program that the IMF has made has shrunk the victim economy. No austerity program has ever helped an economy grow. No budget surplus has ever helped an economy grow, because a budget surplus sucks money out of the economy.
As for the conditionalities, the so-called reforms, they are an Orwellian term for anti-reform, for cutting back pensions and rolling back the progress that the labor movement has made in the last half century. So, the lenders knew very well that Greece would not grow, and that it would shrink.
So, the question is, why does this junk economics continue, decade after decade? The reason is that the loans are made to Greece precisely because Greece couldn’t pay. When a country can’t pay, the rules at the IMF and EU and the German bankers behind it say, don’t worry, we will simply insist that you sell off your public domain. Sell off your land, your transportation, your ports, your electric utilities.
[..] If Greece continues to repay the loan, if it does not withdraw from the euro, then it is going to be in a permanent depression, as far as the eye can see. Greece is suffering the result of these bad loans. It is already in a longer depression today, a deeper depression, than it was in the 1930s.
[..] when Greece fails, that’s a success for the foreign investors that want to buy the Greek railroads. They want to take over the ports. They want to take over the land. They want the tourist sites. But most of all, they want to set an example of Greece, to show that France, the Netherlands or other countries that may think of withdrawing from the euro – withdraw and decide they would rather grow than be impoverished – that the IMF and EU will do to them just what they’re doing to Greece.
So they’re making an example of Greece. They’re going to show that finance rules, and in fact that is why both Trump and Ted Malloch have come up in support of the separatist movement in France. They’re supporting Marine Le Pen, just as Putin is supporting Marine Le Pen. There’s a perception throughout the world that finance really is a mode of warfare.
Sharmini Peries: Greece has now said, no more austerity measures. We’re not going to agree to them. So, this is going to amount to an impasse that is not going to be resolvable. Should Greece exit the euro?
MICHAEL HUDSON: Yes, it should, but the question is how should it do it, and on what terms? The problem is not only leaving the euro. The problem really is the foreign debt that was bad debt that it was loaded onto by the Eurozone. If you leave the euro and still pay the foreign debt, then you’re still in a permanent depression from which you can never exit. There’s a broad moral principle here: If you lend money to a country that your statistics show cannot pay the debt, is there really a moral obligation to pay the debt? Greece did have a commission two years ago saying that this debt is odious. But it’s not enough just to say there’s an odious debt. You have to have something more positive.
[..] what is needed is a Declaration of Rights. Just as the Westphalia rules in 1648, a Universal Declaration that countries should not be attacked in war, that countries should not be overthrown by other countries. I think, the Declaration of International Law has to realize that no country should be obliged to impose poverty on its population, and sell off the public domain in order to pay its foreign creditors.
[..] the looming problem is that you have to pay debts that are so far beyond your ability to pay that you’ll end up like Haiti did after it rebelled after the French Revolution.
[..] A few years after that, in 1824, Greece had a revolution and found the same problem. It borrowed from the Ricardo brothers, the brothers of David Ricardo, the economist and lobbyist for the bankers in London. Just like the IMF, he said that any country can afford to repay its debts, because of automatic stabilization. Ricardo came out with a junk economics theory that is still held by the IMF and the European Union today, saying that indebted countries can automatically pay.
Well, Greece ended up taking on an enormous debt, paying interest but still defaulting again and again. Each time it had to give up more sovereignty. The result was basically a constant depression. Slow growth is what retarded Greece and much of the rest of southern Europe. So unless they tackle the debt problem, membership in the Eurozone or the European Union is really secondary.
There is no such question as “why did austerity fail ‘in a particular case'”?. Austerity always fails. You could perhaps come up with a theoretical example in which a society greatly overspends and toning down spending might balance some things, but other than that, and nothing in what we see today resembles such an example, austerity can only work out badly. And that’s before, as Michael Hudson suggests, austerity is used as a means to conquer people and countries in a financial warfare setting.
This is because our economies (as measured in GDP) are 60-70% dependent on consumer spending. Ergo, when you force consumer spending down through austerity measures, GDP must and will of necessity come down with it. And if you cut spending, stores will close, and then their suppliers will, and they will fire their workers, which will further cut consumer spending etc. It doesn’t get simpler than that.
There is a lot of talk about boosting exports etc., but exports make up only a relatively small part of most economies, even in the US, compared to domestic consumption. As still is the case in virtually every economy, more exports will never make up for what you lose by severely cutting wages and pensions while at the same time raising taxes across the board (Greek reality). The only possible result from this is misery and lower government revenues, in a vicious circle, dragging an economy ever further down.
Since this is so obvious a 5-year old can figure it out in 5 minutes, the reason for imposing the kind of austerity measures that the Eurogroup has unleashed upon Greece must inevitably be questioned in the way professor Hudson does. If someone owes you a substantial amount of money, the last thing you want to do is make sure they cannot pay it back. You want such a person to have a -good- job, a source of income, that pays enough so that they can pay you back. Unless you have your eyes on their home, their car, their daughters, their assets.
What the EU and IMF do with Greece is the exact opposite of that. They’re making sure that Greece gets poorer every day, and the Greeks get poorer, ensuring that the debt, whether it’s odious or not -and that is a very valid question-, will never be paid back. And then they can move in and snap up all of the country’s -rich- resources on the cheap. But in the process, they create a very unstable country, something that may seem to be to their benefit but will blow up in their faces.
It’s not the first time that I say the EU and the US would be well advised to ensure Greece is a stable society, but they all continue to forcibly lead the cradle of democracy in the exact opposite direction.
The best metaphor I can think of is: Austerity is like bloodletting in the Middle Ages, only with a lower success rate.




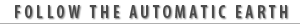




Home › Forums › Austerity Kills. And Then Some.